松弛因子对SOR法收敛速度的影响之C++实现

一、问题描述

用SOR法求解方程组Ax=b, 其中

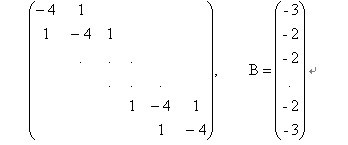
要求程序中不存系数矩阵A,分别对不同的阶数取w=1.1, 1.2, ...,1.9进行迭代，记录近似解x^(k)达到||x^(k)-x^(k-1)||<10^-6时所用的迭代次数k，观察松弛因子对收敛速度的影响，并观察当w <= 0或 w>=2会有什么影响？

二、计算结果与分析

(1) 在收敛标准||x^(k)-x^(k-1)||<e=10^-6且最大迭代次数200前提下，分别取阶数n=5、20、35、50、65、80，取w=1.1, 1.2, ...,1.9进行SOR法迭代求解，计算结果见图1：

图1不同阶数下松弛因子w对收敛速度的影响(w=1.1, 1.2, ...,1.9)

从图1的计算结果可以看出，在w=1.1, 1.2, ...,1.9范围内，不同阶数时SOR法的收敛速度均随收敛松弛因子w的增加而减慢，但在该参数条件下SOR法均能达到收敛要求。

(2) 为观察w£0或w³2时w对收敛速度的影响，在收敛标准||x^(k)-x^(k-1)||<e=10^-6且最大迭代次数250前提下，分别取阶数n=5、20、35、50、65、80，分别取w=-0.5, -0.4, ...,0和w=2, 2.1, ...,2.5进行SOR法迭代求解，计算结果见图5、图6：

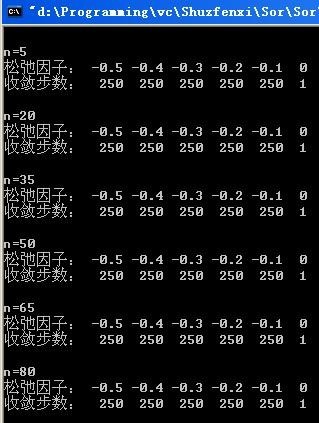
图2 不同阶数下松弛因子w对收敛速度的影响(w=-0.5, -0.4, ...,0)

图3 不同阶数下松弛因子w对收敛速度的影响(w=2, 2.1, ...,2.5)

从图2和图3可看出，当松弛因子w£0或w³2时，不同阶数下SOR法均迭代到了最大收敛次数，这实际上意味着该参数条件下SOR法是发散的(w=0时迭代次数为1是因为此时实际上迭代公式的残量为0，迭代无意义)。

图4给出了在w<0和w>2时SOR法求解的两个特例，显然，迭代到250次时解已趋于无限，这正式迭代发散的表现。

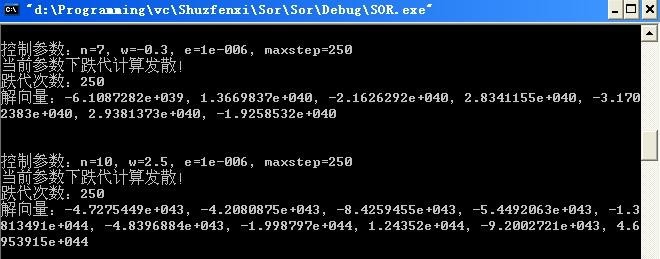
图4w<0和w>2时SOR法求解的两个特例

综上所述，对于题目给出的线性方程组来说，当松弛因子w=1.1, 1.2, ...,1.9时，SOR法迭代求解是收敛的，而当w£0或w³2时SOR法是发散的。这实际上与教材中的定理很好的符合，即0<w<2是SOR法收敛的必要条件。

三、源代码

#include "stdafx.h"
#include <math.h> 
#include<iostream>
using namespace std;
#include <iomanip> 

int SOR(int n,double w,double e=1e-6,int maxstep=100,int displaytype=0)
//SOR法求解题3子函数，n:阶数,w:松弛因子，e:收敛阈值，maxstep：最大收敛步数，返回值为收敛步骤数，displaytype：是否显示计算结果,0:不显示，非零：显示
{
int i,j,m;
double delta;
double s,t;
double *px=new double [n];//分配解向量空间
for(i=0;i<n;i++)px[i]=0;//解向量赋初值
m=0;//当前跌代次数赋初值0

if (n<=2)
{
 cout<<"阶数过小！"<<endl;
 return 0;
}
do 
{
 delta=0;//当前跌代误差赋初值0
 
 ///////////////////第1行计算////////////////////////////
 s=px[0];
 t=-4*px[0]+px[1];
 px[0]=(-3-t)*w/(-4)+s;
 delta+=(px[0]-s)*(px[0]-s);// (px[0]-s)>=0?(px[0]-s):(-px[0]+s);
 ///////////////////第2至n-1行计算//////////////////////
 for (i=1;i<=n-2;i++)
 {
 s=px[i];
 t=px[i-1]-4*px[i]+px[i+1];
 px[i]=(-2-t)*w/(-4)+s;
 delta+= (px[i]-s)*(px[i]-s);//(px[i]-s)>=0?(px[i]-s):(-px[i]+s);
 }
 ///////////////////第n行计算////////////////////////////
 s=px[n-1];
 t=px[n-2]-4*px[n-1];
 px[n-1]=(-3-t)*w/(-4)+s;
 delta+=(px[n-1]-s)*(px[n-1]-s); //(px[n-1]-s)>=0?(px[n-1]-s):(-px[n-1]+s);
 delta=(double) sqrt((double)delta);
 m+=1;//跌代次数加1
}
while((delta>e)&&(m<maxstep));

/////////////////////结果输出//////////////////////////////
if (displaytype!=0)
{
cout<<endl<<"控制参数：n="<<n<<"，w="<<w<<"，e="<<e<<"，maxstep="<<maxstep<<endl;
if ((delta>e)&&(m>=maxstep))cout<<"当前参数下跌代计算发散！"<<endl;
cout<<"跌代次数："<<m<<endl<<"解向量：";
cout<<setprecision(8);//设置解向量输出精度为8位 
for(i=0;i<n-1;i++)cout<<px[i]<<"，";
cout<<px[n-1]<<endl<<endl;
}
delete [] px;
//if ((delta>e)&&(m>=maxstep))return -m;
return m;
}

int _tmain(int argc, _TCHAR* argv[])
{
   int   n=5; //阶数
   double w=1.5;//松弛因子
   double e=1e-6;//收敛阈值
   int maxstep=250;//最大收敛步数
  
  ////////////////不同阶数 w=1.1--1.9范围时w对收敛步数的影响///////////////////////////
   for (n=5;n<85;n+=15)
   {
     cout<<endl<<"n="<<n<<endl; 
	  if (n==5) cout<<"松弛因子：";
	  else cout<<"松弛因子： ";
	 
	  for(w=1.1;w<2.0;w+=0.1)cout<<w<<" ";
	  cout<<endl;
	  cout<<"收敛步数：";
	 for(w=1.1;w<2.0;w+=0.1)
	 {
		 cout<<" "<<SOR(n,w, e,maxstep)<<" ";
	 }
   cout<<endl;  
   }

///////////////////////不同阶数 w<=0和w>2时w对收敛步数的影响////////////////////////


 //w<=0
  cout<<setprecision(3);//设置解向量输出精度为8位 
 for (n=5;n<85;n+=15)
   {
     cout<<endl<<"n="<<n<<endl; 
	  cout<<"松弛因子： ";
	  for(w=-0.5;w<=-0.1;w+=0.1)cout<<w<<" ";
	  cout<<" 0"<<endl;
	  cout<<"收敛步数： ";
	 for(w=-0.5;w<=0;w+=0.1)
	 {
		 cout<<" "<<SOR(n,w, e,maxstep)<<" ";
	 }
   cout<<endl;  
   }

 //w>=2
   for (n=5;n<85;n+=15)
   {
     cout<<endl<<"n="<<n<<endl; 
	 cout<<"松弛因子：   ";
	 
	  for(w=2;w<2.6;w+=0.1)cout<<w<<"  ";
	  cout<<endl;
	  cout<<"收敛步数：";
	 for(w=2;w<2.6;w+=0.1)
	 {
		 cout<<" "<<SOR(n,w, e,maxstep)<<" ";
	 }
   cout<<endl;  
   }

   //特定数据点
SOR(7,-0.3, e,maxstep,1);
SOR(10,2.5, e,maxstep,1);

   return 0;
}